In part 2 we explore the origin of imaginary/lateral numbers. Like many breakthroughs in math and science, this one comes as a results of existing methods not quite working as they should. Even though the square roots of negative numbers have been reported to show up since first century AD, they were easily ignored and dismissed as the problem's way of saying there are no solutions.
It wasn't until serious solutions to cubic equations showed up on the scene in the 1500s that mathematicians we're compelled to take \(\sqrt{-1}\) seriously. And it's not because they wanted to. Cardan was aware that using\(\sqrt{-1}\) did have some utility, but called such solutions sophistic (subtly deceptive reasoning or argumentation). Just like negative numbers and zero before them, \(\sqrt{-1}\) was mistrusted because it didn't seem to be related to anything physical. As we'll see next time, the only reason \(\sqrt{-1}\) began to gain traction was because it allows us to beautifully and elegantly find the solutions to cubic equations.
A LITTLE CLARIFICATION REGARDING CUBIC ROOT FINDING
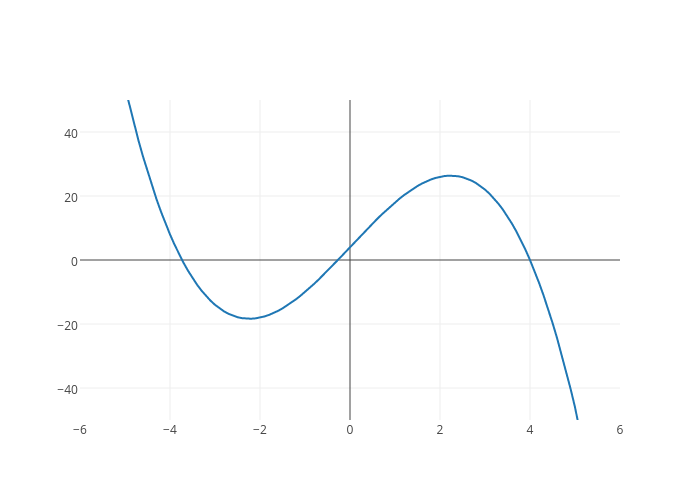
Using the cubic x^3 = 15x + 4.
In part two I make pretty heavy use of the cubic $$x^3 = 15x + 4.$$
This cubic originally showed up in the work of an important character we'll meet in part 3, Rafael Bombellli. A pivotal part of my argument is that cubics must have at least one real root because of they way they're shaped (more specifically because of their end behavior). As you may already know, cubics can have up to 3 real roots - and if we plot our example, we see that this case does have three real roots.
$$f(x) = -x^3 + 15x + 4$$
I was a bit concerned about the legitimacy of the argument that since our function must cross the x-axis at lease once, the del Ferro-Tartaglia-Cardan formula must hold up (see below for full derivation):
$$ x^3 + cx = d\\ x = \sqrt[3]{\frac{d}{2} + \sqrt{\frac{d^2}{4}-\frac{c^3}{27}}} - \sqrt[3]{-\frac{d}{2} + \sqrt{\frac{d^2}{4}-\frac{c^3}{27}}}$$
After all, if the function only did have one real root, it seems the above formula may just yield the imaginary roots. If we try the quick example \( x^3=3x+20\), plugging into the above formula we obtain \(x = \sqrt[3]{10+3\sqrt{11} }- \sqrt[3]{-10+3\sqrt{11} }\) which comes out to \(x=3.08085946\), which is the real root of the equation. So it's fair to say that under certain conditions and when there is only one real root, our formula will find it. Something I'm not quite clear about here is if this formula will always find the real root, or if it will sometimes yield the imaginary roots.
In the video I gloss over things a bit for the sake of clarity - Cardan and his contemporaries likely knew that a function like \(x^3 = 15x + 4\) would have three real roots - and in the end, this may have been more compelling to them than just knowing that all cubics must have at least one real root.
A PROPER DERIVATION OF THE DEL FERRO'S SECRET FORMULA
Solving for x in linear, quadratic, and cubic equations.
It's hard to imagine how del Ferro must have felt after discovering the solution to his cubic equation - he was arguably the only person on the planet who knew how to solve equations like this. The part of the video were I show the derivation his cubic formula goes pretty fast, so I've included a proper derivation here.
$$x^3 + cx = d$$
let \(x = u+v\)
$$(u+v)^3 + c(u+v) = d \\(u^2 + 2uv + v^2)(u+v) + c(u+v) = d\\(u^3 + 3u^2v + 3uv^2 + v^3) + c(u+v) = d\\u^3 + v^3 + 3uv(u+v) + c(u+v) = d\\u^3 + v^3 + (3uv + c)(u+v) = d\\$$
This part is a little strange, from what I've read, this is supposed to be del Ferro's deep insight - it seems a little hacky to me! If we let \(3uv + c = 0\), then \(u^3 + v^3 = d\) and \(v = \frac{-c}{3u}\).
$$u^3 + \big(\frac{-c}{3u}\big)^3 = d \\u^3 - \frac{c^3}{27u^3} - d = 0 \\u^6 - du^3 - \frac{c^3}{27} = 0$$
let \(z = u^3\)
$$z^2 - dz - \frac{c^3}{27} = 0$$
Now using the quadratic formula:
$$z = \frac{d \pm \sqrt{(-d)^2-(4)(1)(\frac{-c^3}{27}})}{2} \\z = \frac{d}{2} \pm \frac{\sqrt{d^2+\frac{4c^3}{27}}}{2} \\z = \frac{d}{2} \pm \frac{\sqrt{d^2+\frac{4c^3}{27}}}{\sqrt{4}} \\z = \frac{d}{2} \pm \sqrt{\frac{d^2}{4}+\frac{4c^3}{(27)(4)}} \\z = \frac{d}{2} \pm \sqrt{\frac{d^2}{4}+\frac{c^3}{27}} \\$$
now substituting back in \(z = u^3\):
$$u^3 = \frac{d}{2} \pm \sqrt{\frac{d^2}{4}+\frac{c^3}{27}} \\u = \sqrt[3]{\frac{d}{2} \pm \sqrt{\frac{d^2}{4}+\frac{c^3}{27}}} \\$$
from above,
$$u^3 + v^3 = d \\v^3 = d-u^3 \\$$
Only consider positive root (using the negative root will result in the same exact answer):
$$v^3 = d - \bigg[\frac{d}{2} + \sqrt{\frac{d^2}{4}+\frac{c^3}{27}}\bigg]\\v^3 = \frac{d}{2} - \sqrt{\frac{d^2}{4}+\frac{c^3}{27}}\\x = u + v \\x = \sqrt[3]{\frac{d}{2} + \sqrt{\frac{d^2}{4}+\frac{c^3}{27}}} + \sqrt[3]{\frac{d}{2} - \sqrt{\frac{d^2}{4}+\frac{c^3}{27}}}$$
We can also obtain another perfectly valid version of the formula by factoring out a \(\sqrt[3]{-1} = -1\) from the second term:
$$ x = \sqrt[3]{\frac{d}{2} + \sqrt{\frac{d^2}{4}+\frac{c^3}{27}}} - \sqrt[3]{-\frac{d}{2} + \sqrt{\frac{d^2}{4}+\frac{c^3}{27}}}$$
This is the formula del Ferro derived. It's crazy to think that ~500 years ago only one person on the planet knew this formula - and he had no idea it would lead to the development and acceptance of imaginary numbers. We end up focusing on a slightly different cubic, introduced later by Cardan:
$$x^3 = cx + d$$
Note that this rearrangement changes the sign of c. Substituting \(-c\) for \(c\) into our final result above, we obtain:
$$x = \sqrt[3]{\frac{d}{2} + \sqrt{\frac{d^2}{4}-\frac{c^3}{27}}} - \sqrt[3]{-\frac{d}{2} + \sqrt{\frac{d^2}{4}-\frac{c^3}{27}}}$$
Just as above, we can factor out a \(\sqrt[3]{-1} = -1\) from the second term to obtain the equivalent formula:
$$x = \sqrt[3]{\frac{d}{2} + \sqrt{\frac{d^2}{4}-\frac{c^3}{27}}} + \sqrt[3]{\frac{d}{2} - \sqrt{\frac{d^2}{4}-\frac{c^3}{27}}}$$
This is version of the cubic formula that will ultimately lead us into issues with \(\sqrt{-1}\), as shown in the video.
WORKS CITED
An Imaginary Tale: The Story of sqrt(-1) - Paul J. Nahin Nahin's book has proven incredibly helpful through the process of creating this series, I highly recommend it for those looking to go deeper into imaginary numbers.